Graph Drawing with Low Visual Complexity

Algorithms for drawing graphs try to optimize (or give a guarantee) on certain formal quality measures. Typical measures include avoiding edge crossings, avoiding small angles between adjacent or crossing edges and minimizing the ratio between the largest and the smallest distance between any pair of points. Ideally, edges are represented by straight-line segments, but often also polygonal chains or circular arcs are used. When using polygonal chains, one usually tries to minimize the number of bends.

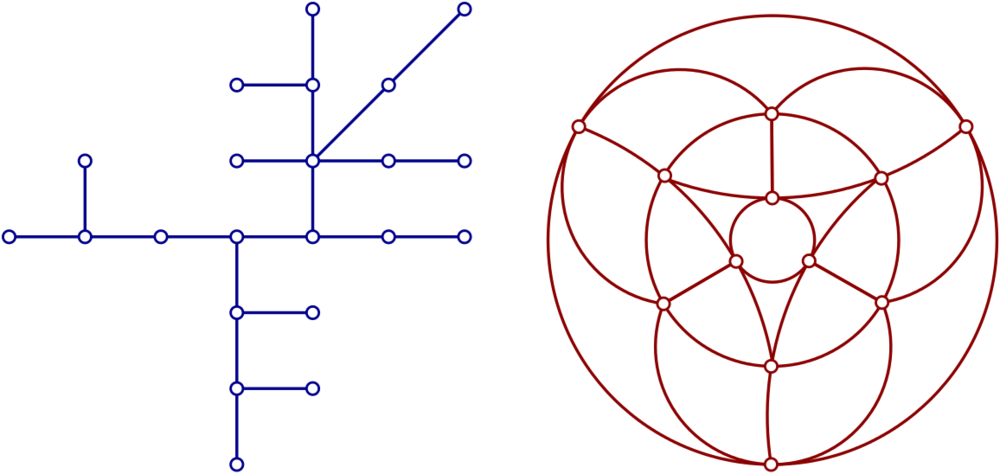
In this project, we want to examine a new conceptual design. The task is to draw a graph with a minimum number of geometric primitive. For example, we can draw a path in a graph as a single straight-line segment. The vertices are then only represented by crossings (or touching points) with other geometric elements. We call the number of used primitives the visual complexity of a drawing. We want to investigate how to create drawings with low visual complexity and find bounds for the required number. We want to answer this question for several classes of planar graphs, for example trees, series-parallel graphs, planar 3-trees and trangulations. As geometric primitive, we want to use mainly segments and circular arcs.