Keypoint Detection in 3D Point Clouds

Jens Garstka, Gabriele Peters

Publication:

• Jens Garstka and Gabriele Peters,
  Highly Parallelizable Algorithm for Keypoint Detection in 3-D Point Clouds, in: Informatics in Control, Automation and Robotics 12th International Conference (ICINCO 2015), Revised Selected Papers, Lecture Notes in Electrical Engineering, Vol. 383, pp. 267-285, Springer, 2016.
• Jens Garstka and Gabriele Peters,
  Fast and Robust Keypoint Detection in Unstructured 3-D Point Clouds, 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2015), Colmar, France, July 21-23, 2015.
  ► best paper award

All publications are available from Publications.

Summary

3D scene understanding is necessary for interaction in the environment. For that purpose the classification of 3D objects is essential. The detection of keypoints in 3D point clouds often constitutes the first step for an efficient and reliable classification of objects.

We proposed a fast and robust method for an automatic identification of keypoints in unstructured 3D point clouds and compared it with other state-of-the-art keypoint detection algorithms on a number of 3D objects. Our approach yielded a considerably faster computation and outperformed other methods in terms of relative repeatability of keypoints under rotation. Other advantages consist in its stable behavior in the presence of noise and a moderate scale invariance, which is particularly useful, if keypoints are supposed to be used with any arbitrary local descriptor to classify point clouds at different scales.

Possible fields of applications besides autonomous systems are 3D object retrieval or appropriate descriptions of 3D data in general.

Major Steps of the Algorithm

1. Convert point cloud to a solid voxelized volume

This neither requires additional surface information or normals nor needs to approximate them.

• Left: 3D object Bunny (from the Stanford Computer Graphics Laboratory).
• Right: Voxel representation of a depth scan point cloud. Blue dots: voxels corresponding to 3D points. Red dots: filled voxels below the surface.

2. Convolve voxelized volume with a spherical kernel

Two examples for convolution results. Shown voxels contain 3D points from the initial point cloud. Convolution values are color-coded: red: small, green: medium; blue: large.

• Left: Convolution result from a depth scan point cloud.
• Right: Convolution result from a closed model point cloud.

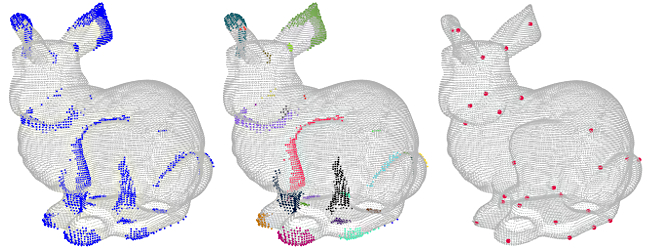
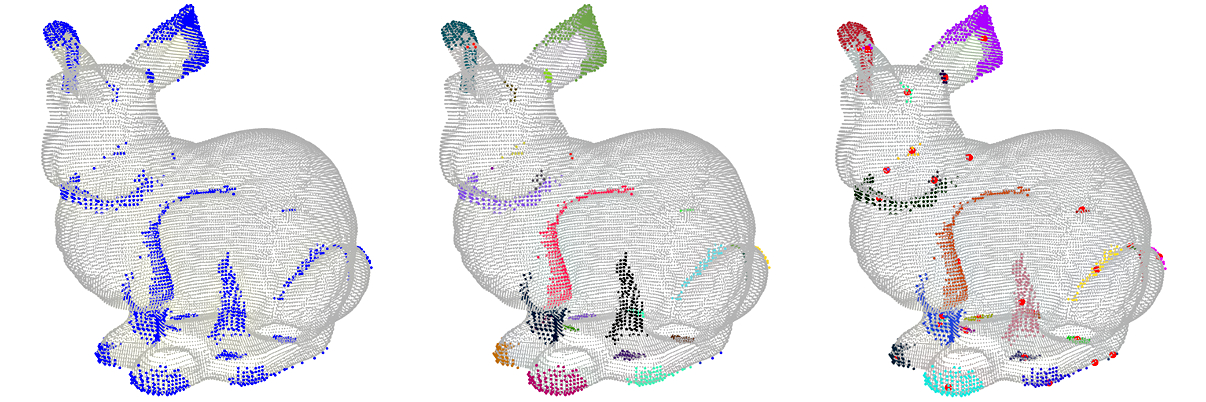
3. From the intitial point cloud choose representatives of points for rare convolution responses as keypoints

This is done via building histograms of convolution results, clustering, and finding nearest neighbours to cluster centroids.

• Left: Blue points are keypoint candidates, i.e., keypoints with rare convolution values.
• Middle: Different clusters are displayed in different colors.
• Right: Red points are the final keypoints.

Further Examples

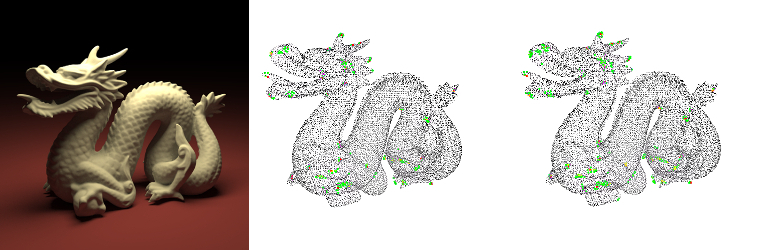
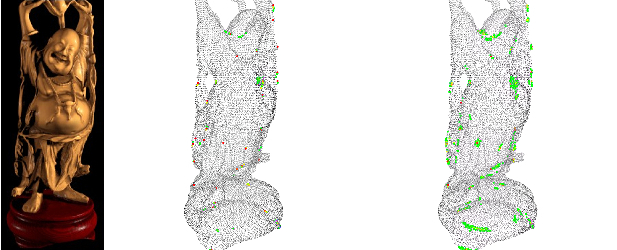
Two further 3D models from the Stanford Computer Graphics Laboratory, Dragon and Happy Buddha. Middle and Right: Point clouds with superimposed keypoint candidates. From red to green: stronger to weaker candidates. (Click on images for larger point clouds.)

• Left: Model of the 3D object.
• Middle: Keypoint candidates calculated from original point cloud.
• Right: Keypoint candidates calculated from point cloud with added noise.

Comparison with State-of-the-Art Algorithms

We compared our approach with 4 other state-of-the-art keypoint detection algorithms in terms of repeatability under rotation and computation time. We picked a total of 50 point clouds from 5 object classes from the object data base of [Lai et al., 2011], each point cloud was rotated by 4 different angles, and on each resulting point cloud we ran our algorithm.

Examples for objects from the chosen classes "cap", "greens", "kleenex", "scissors", and "stapler" from [Lai et al., 2011]

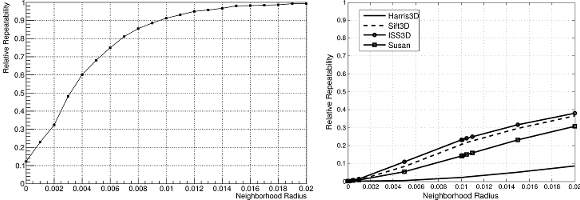
Repeatability under Rotation

Relative repeatability (vertical axis), i.e., portion of detected keypoints in the rotated cloud, that falls into a neighbourhood (horizontal axis) of a keypoint in the unrotated cloud

• Left: Rotation of 35 degrees, our approach.
• Right: Rotation of 35 degrees, four other state-of-the-art algorithms (Harris3D, Sift3D, ISS3D, Susan).

Computation Time

The presented algorithm is designed to be highly parallelizable and can thus be executed fast. For example, under a standard system configuration we obtained the following average execution times for the computation of the keypoints of one 3D point cloud:

• ISS3D: 1197 ms
• Harris3D: 1010 ms
• Our Approach: 457 ms

Noise

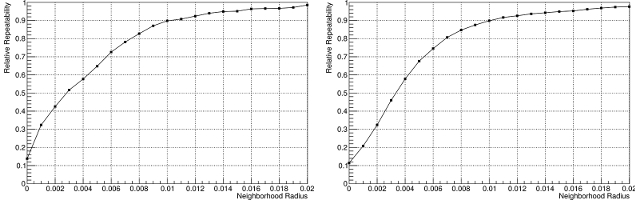
The proposed approach is robust to noise. We added noise to the point clouds at a level of 0.5 times the cloud resolution.

• Left: Relative repeatability for a rotation of 15 degrees on original point clouds.
• Right: Relative repeatability for a rotation of 15 degrees on point clouds with added noise. Almost no loss in performance is recognizable.

Best Paper Award at ICINCO 2015 in Colmar

Jens Garstka (left) receiving the best paper award, with Oleg Gusikhin