Computational Intelligence - Local Input Space Histograms

Cover of Informatik Spektrum, Vol. 38(4), 2015

Jochen Kerdels, Gabriele Peters

Publications:

• Jochen Kerdels and Gabriele Peters,
  Analysis of High-Dimensional Data Using Local Input Space Histograms, Neurocomputing, Vol. 169, pp. 272-280, 2015.
  [pdf | pdf supplem. material | doi]
• Jochen Kerdels and Gabriele Peters,
  Supporting GNG-based Clustering with Local Input Space Histograms, Proceedings of the 22nd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (559-564), 2014.
  [pdf]
• Jochen Kerdels and Gabriele Peters,
  Clustering hochdimensionaler Daten, Informatik Spektrum, Springer, Vol. 38(4), cover art, p. 335, 2015.

Summary

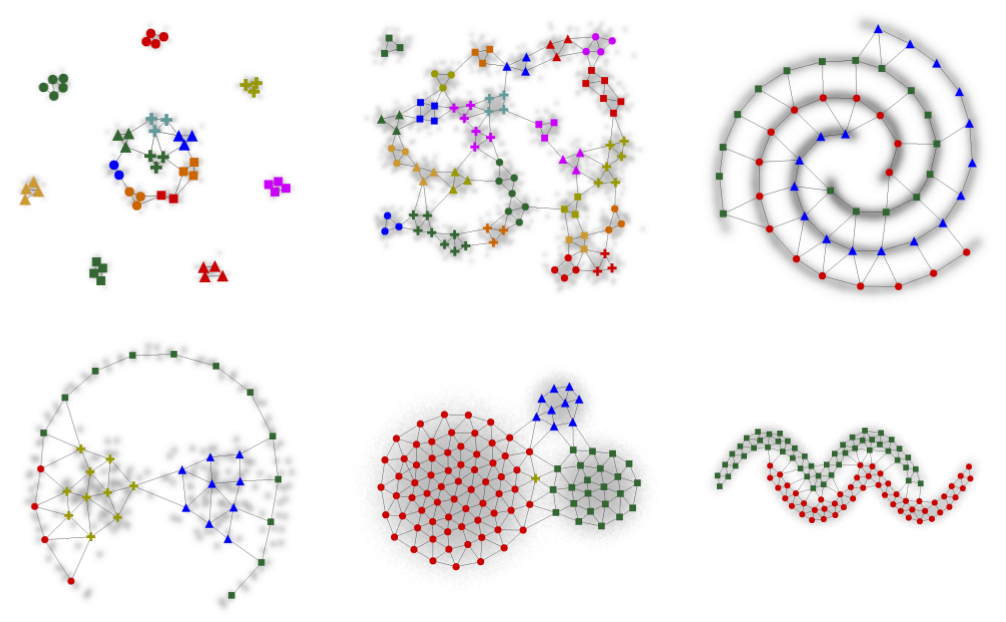
In recent years the ability to store and process vast amounts of data has increased considerably. One approach to discover structure in this kind of data is the use of methods that employ forms of unsupervised competitive learning such as the growing neural gas (GNG) introduced by Bernd Fritzke in 1995. GNGs are topology representing networks that approximate the structure of an input space using an unsupervised, data-driven growth process. Individual units in a GNG network represent local regions of the input space as convex polyhedrons. As a consequence, complex structures of an input space, e.g., non-convex clusters, can only be approximated piecewise by a larger number of units.
This piecewise representation of input space structures makes it often difficult to recover the relationship between the network units and the corresponding structures in input space. To support the reconstruction of such relationships we proposed Local Input Space Histograms (LISH) as an extension to the original GNG algorithm.

Local Input Space Histograms

Local Input Space Histograms

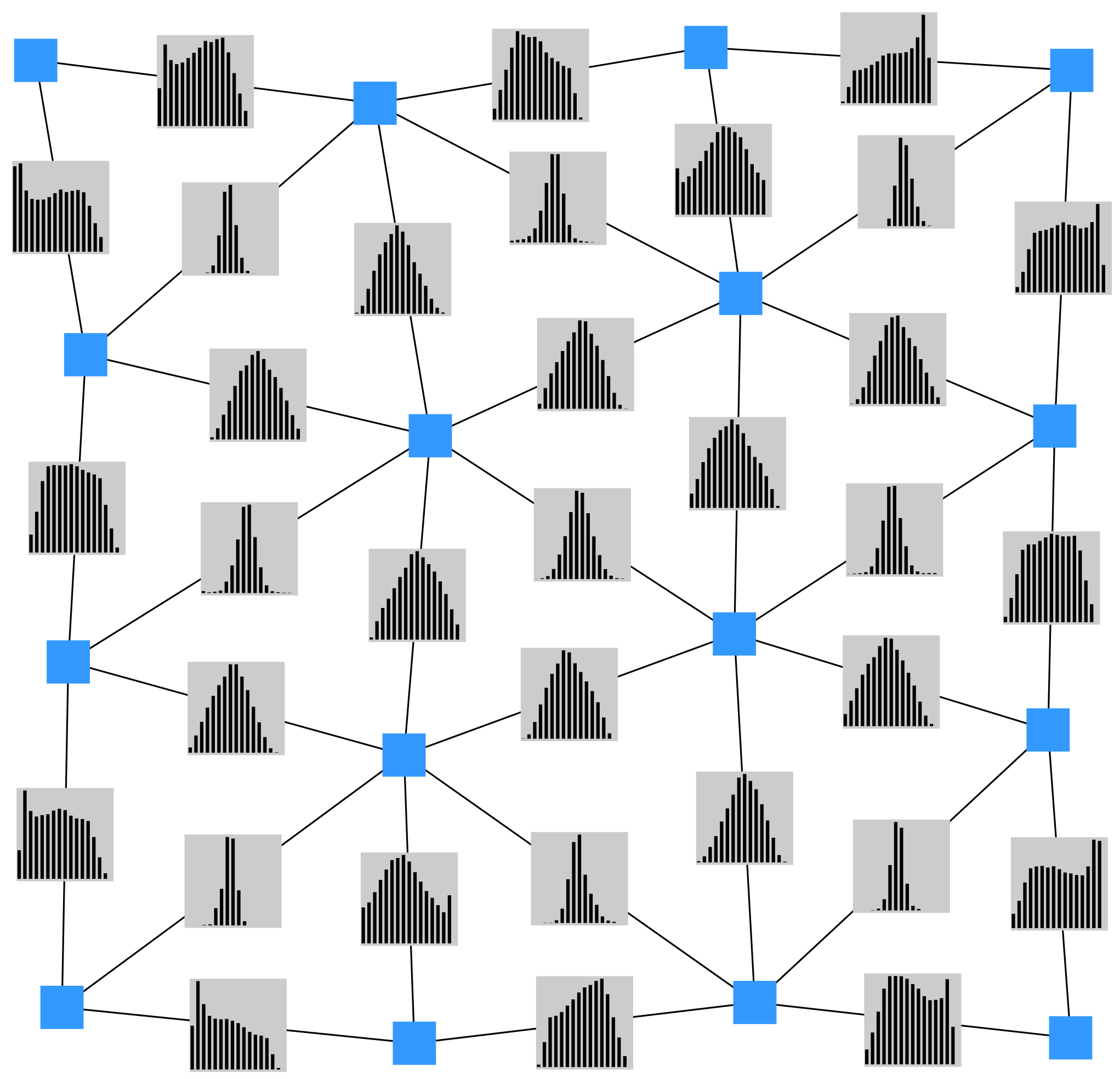
In order to gather more information about the input space structure that underlies a particular growing neural gas we augmented each GNG edge with a small histogram. The histograms capture the local distribution of inputs relative to the GNG units that are connected by an edge.

Based on this additional information it becomes possible to infer certain properties of the input space that were previously unattainable. For instance, it can be estimated if the input space between two GNG units is either densely or sparsely populated. This information can be used, e.g., to guide clustering approaches that group GNG units into higher order entities that directly correspond to complex input space structures.

Right: Local Input Space Histograms occurring in a uniform, two-dimensional input space.

Bottom: Example of a complex, two-dimensional input space (grey colors) that was approximated by a GNG network. Local input space histograms are shown for two edges of the GNG.

Hierarchical Clustering of High Dimensional Data

The additional information provided by LISH can also be used to guide the hierarchical clustering of data. In this case the distance between two GNG units is not determined by the distance between the corresponding reference vectors or prototypes, but is instead based on the average bin error of the LISH at the respective edge.

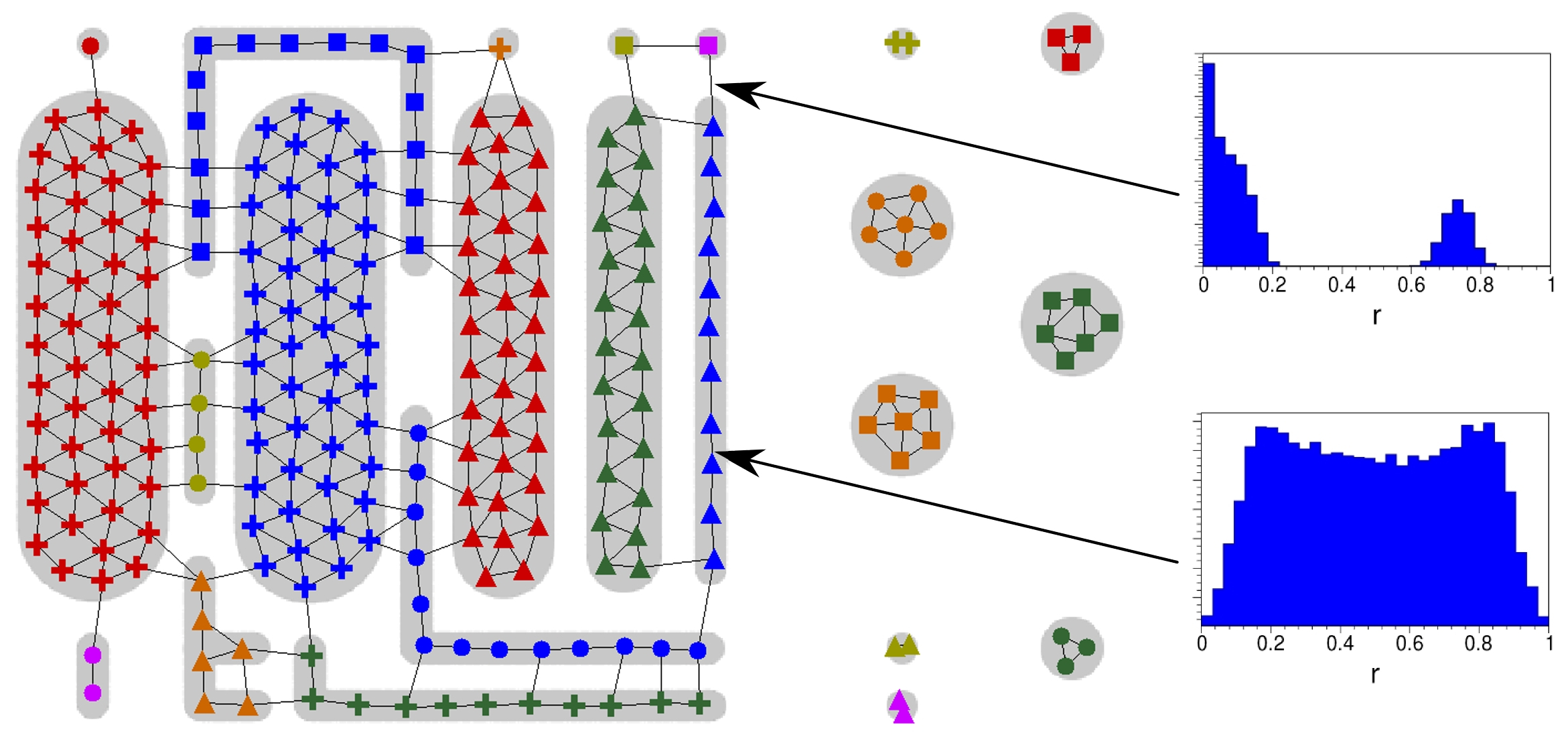
Force-Based Graph Drawing

Another application area in which the LISH information in a GNG can improve existing approaches is graph drawing. In this case the individual GNG edges are extended with a weight parameter that is determined using the average bin error of the particular LISH. This edge weight is then used as a proxy for the attraction between GNG units in a force-based graph drawing of the GNG. In addition, the weight also determines the color and thickness of the respective edge in the resulting drawing.