Das Färbungsproblem in der Betriebswirtschaftslehre

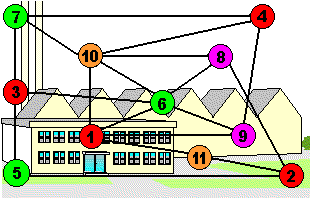
Problemformulierung

Gegeben sei ein ungerichteter Graph G=(V,E) mit Knotenmenge V und Kantenmenge E. Die Knoten von G heißen zulässig gefärbt, wenn jedem Knoten eine Farbe so zugeordnet ist, dass die Knoten, die durch eine Kante verbunden sind, nicht dieselbe Farbe tragen. Man spricht auch vereinfachend von der Färbung des Graphen. Eine triviale Färbung erhält man, wenn jedem Knoten eine andere Farbe zugewiesen wird; bei n Knoten benötigt man genau n Farben. Interessant sind nun genau die zulässigen Färbungen, bei denen möglichst wenig Farben verwendet werden. Das Minimum der für eine zulässige Färbung von G erforderlichen Farben heißt die chromatische Zahl .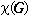

JavaScript-Applikation »Zeitplanung als Färbungsproblem«

Der Lehrstuhl für Operations Research organisiert einen Workshop „Conditionals, Information, and Inference“, zu dem zahlreiche Fachleute aus dem In- und Ausland als Gastredner eingeladen sind. Die Beiträge dieser Wissenschaftler sind eingereicht und deren Themen im Internet bekannt gegeben. 10 der ca. 100 insgesamt erwarteten Teilnehmer/innen sind Honoratioren, denen man die Möglichkeit einräumt anzugeben, welche Vorträge Sie auf keinen Fall verpassen möchten. Die Organisatoren müssen nun den Zeitplan so ausarbeiten, dass zwei Vorträge, die ein Ehrengast hören möchte, auf keinen Fall zur selben Zeit statt finden. Außerdem lautet aber auch die Vorgabe, dass durch parallele Sitzungen die Gesamttagungsdauer gestrafft wird.

JavaScript-Applikation »Personalplanung als Färbungsproblem«

Eine kleine Fluggesellschaft hat ihren Stammsitz in Dortmund und fliegt täglich verschiedene Flughäfen innerhalb Europas an. Personalwechsel im Cockpit findet jeweils nur in Dortmund statt, so dass als Flugzeit jeweils die Zeit zwischen Abflug und Rückkehr eines Fliegers betrachtet werden muss. Insgesamt müssen acht Flüge, deren Zeiten frei wählbar sind, mit Personal besetzt werden. Ziel ist es, die Anzahl der insgesamt benötigten Crews zu minimieren.

Applet-Seite

Zum Ampelproblem wurde von uns ein Applet programmiert, mit dem Sie einmal selbst die Einfärbung eines Graphen vornehmen können, um eine Ampelschaltung mit konfliktfreien Grünphasen zu generieren.

Ampelschaltung

Die Ampeln stellen die Knoten im Graphen dar. Zwei Ampeln, die nicht gleichzeitig GRÜN zeigen dürfen, sind durch Kanten im Graphen verbunden. Eine Phase ist durch eine bestimmte Ampelschaltung charakterisiert. Eine solche Schaltung heißt dann zulässig, wenn die freigegebenen Wege nicht zu Verkehrskonflikten auf der Kreuzung führen. Versuchen Sie nun mit dem von uns programmierten Applet einmal selbst, eine möglichst gute Färbung eines Graphen zu finden.

Frequenzblockzuweisung im Bereich der Telekommunikation

Die Deutsche Telekom hat ein Softwarepaket zur Verteilung von Sendefrequenzen entwickelt, bei dem auch Tabu Search implementiert ist. Beim digitalen terrestrischen Hörrundfunk werden sechs Stereoprogramme zu einem Programmblock zusammengefasst und in einem Frequenzblock abgestrahlt. Für jedes Verbreitungsgebiet, in der Bundesrepublik können das mehrere Hundert sein, ist ein Frequenzblock erforderlich.
Herr Hackelbörger, Mitarbeiter im Technologiezentrum der Telekom in Darmstadt, gab interessante Erläuterungen [avi, 6MB], von denen Sie einen Ausschnitt hier sehen können. Das vollständige Interview finden Sie auf unserer CD Intelligente Strategien in Theorie und Praxis.

Konfliktfreie Lagerung von Sonderabfällen

Der sachgerechten Lagerung von Chemikalien wird bei Sicherheitsbetrachtungen oft wenig Bedeutung beigemessen, doch Unfälle wie der spektakuläre Lagerbrand bei der Firma Sandoz in Basel 1986 zeigen, dass auch mit der Lagerung schwer kalkulierbare Gefahren verbunden sein können. Kernpunkt der Abbildung des Lagerproblems auf das Graphenfärbungsproblem ist die Unterscheidung von unterschiedlichen Gefahrenklassen, die im Chemikaliengesetz unter Berücksichtigung des individuellen Gefahrengrades festgelegt ist. Ordnet man jeder Klasse einen Knoten im Graphen zu und drückt das Verbot der gemeinsamen Lagerung von Stoffen unterschiedlicher Klassen durch eine entsprechende Kante aus, so ergibt sich - wie Untersuchungen gezeigt haben - für das beschriebene allgemein formulierte Problem ein Graph mit 26 Knoten und 254 Kanten. Mit der vorgenommenen Transformation des Problems sind auch entsprechende Algorithmen anwendbar, die insbesondere für die Konzeption von Lagern und die damit verbundenen Entscheidungen von großer Bedeutung sind.