Zertifikat Mathematische und informatische Grundlagen
Foto: Hardy Welsch
Zertifikate Mathematische und informatische Grundlagen
Abschluss: Zertifikat
Studienbeginn: Winter- oder Sommersemester
ECTS-Punkte: 60
Kosten: ab ca. 900 €, je nach Studiendauer
Zugangsvoraussetzungen: Immatrikulation im B.Sc. Mathematisch-technische Softwareentwicklung (Abitur oder gleichwertige Hochschulzugangsberechtigung oder berufliche Qualifizierung)
Wie ist das Zertifikat Mathematische und informatische Grundlagen aufgebaut?
Um ein Zertifikat zu erhalten müssen Sie insgesamt sieben Module im Gesamtumfang von 60 ECTS-Punkte erfolgreich absolvieren.
Das Zertifikat besteht aus einem Pflichtmodul im Bereich Mathematik, vier Pflichtmodulen im Bereich Informatik sowie einem Wahlpflichtmodul im Bereich Mathematik und einem Wahlpflichtmodul im Bereich Informatik.
Pflichtmodul Mathematik:
- 61111 Mathematische Grundlagen
Bei Pflichtmodulen Informatik ein Paket aus:
Paket I:
- 63811 Einführung in die imperative Programmierung
- 63611 Einführung in die objektorientierte Programmierung
- 63511 Einführung in die technischen und theoretischen Grundlagen der Informatik
- 63118 Datenbanken
Paket II (belegbar ab Wintersemester 2025/26):
- 63017 Datenbanken und Sicherheit im Internet
- 65001 Grundlagen der Informatik 1
- 65002 Grundlagen der Informatik 2
Für das Zertifikat muss entweder Paket I oder Paket II in Gänze absolviert worden sein.
Wahlpflichtmodule:
Im Bereich Mathematik ein Modul aus
Im Bereich Informatik ein Modul aus
Wichtig: Bis wann letztmalig eine Prüfungsteilnahme in diesen Modulen bzw. eine Anerkennung von Leistungen auf diese Module möglich ist, ist in der Modulbeschreibung zu dem jeweiligen Modul ausgeführt.
Mehr Informationen zum Zertifikatsstudium finden Sie im Leitfaden (PDF).
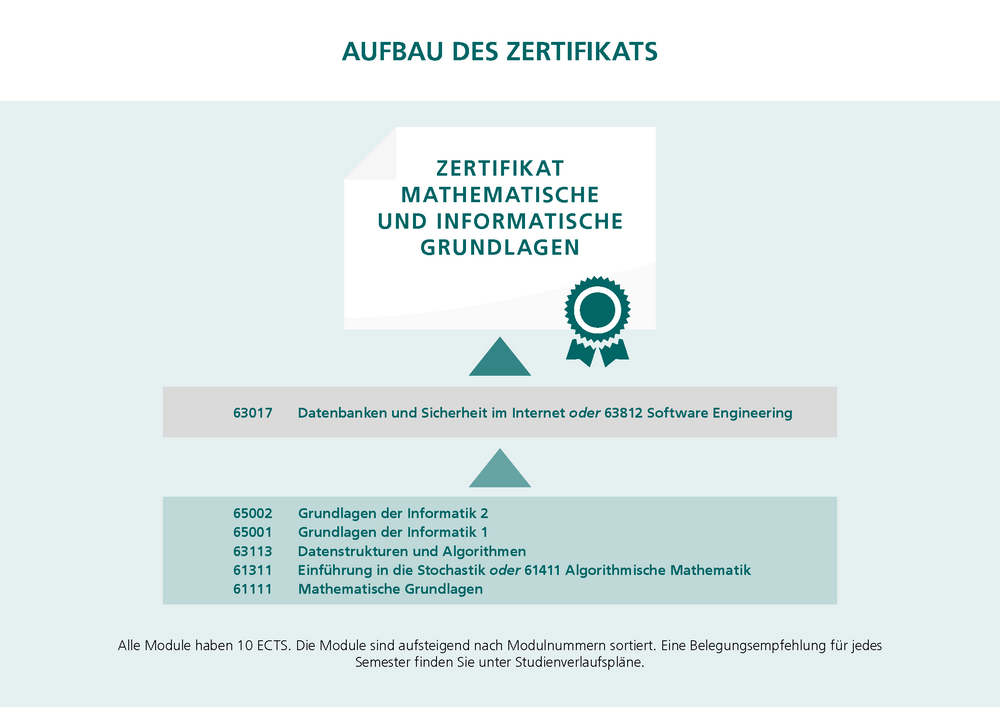Abbildung: FernUniversität in Hagen
Beschreibung der Grafik
mehr Infos
In der Grafik sehen Sie den Aufbau des Studiums, bei dem Sie das Zertifikat Mathematische und Informatische Grundlagen erhalten können. Um ein Zertifikat zu erwerben, müssen Sie insgesamt sieben Module im Gesamtumfang von 60 ECTS-Punkten erfolgreich absolvieren. Zu Beginn des Zertifikatsstudiums schließen Sie folgende Module ab: Mathematische Grundlagen, Einführung in die Stochastik oder Algorithmische Mathematik, Einführung in die imperative Programmierung, Einführung in die objektorientierte Programmierung und Grundlagen der technischen und theoretischen Informatik.
Danach bearbeiten Sie die Module Datenbanken I und entweder Datenstrukturen und Algorithmen oder Software Engineering und schließen diese mit Modulprüfungen ab.
Studienverlaufspläne für das Zertifikat
Nachstehend finden Sie exemplarische Beispiele für die Planung Ihres Zertifikates Mathematische und Informatische Grundlagen. Sie sind auf einen Studienbeginn im Winter- oder im Sommersemester ausgerichtet. Sie sind als Beispiel gedacht und können von Ihnen an Ihre eigenen Interessen und Bedürfnisse angepasst werden. Beachten Sie aber, dass für manche Module formale Voraussetzungen existieren und manche Module inhaltlich von anderen abhängen. Genaue Informationen zu den einzelnen Modulen finden Sie auf der jeweiligen Modulseite.
Wie können Leistungen im Zertifikat anerkannt werden?
Wenn Sie bereits erbrachte Prüfungsleitungen in Ihrem Zertifikatsstudium verwenden möchten, stellen Sie bitte einen Antrag auf Anerkennung. Bitte nutzen Sie dafür das nachstehende Formular. Weitere Informationen finden Sie im Studiengangsportal B.Sc. Mathematisch-technische Softwareentwicklung unter Anerkennung.
Anerkennungsformular für das Zertifikat Mathematische und informatische Grundlagen (PDF)
Wie kann das Zertifikat beantragt werden?
Wenn Sie alle für die Ausstellung eines Zertifikats erforderlichen Module erfolgreich abgeschlossen haben, können Sie das Zertifikat beim Prüfungsamt beantragen. Dafür verwenden Sie bitte folgendes Antragsformular (PDF). Bitte beachten Sie, dass eine Ausstellung des Zertifikats erst ab dem 01.10.2022 erfolgt.
Das vollständig ausgefüllte Antragsformular senden Sie bitte per E-Mail an: pruefungsamt.mathinf
Hinweis: Wenn Sie im Bachelorstudiengang Mathematisch-technische Softwareetwicklung eingeschrieben sind, können Sie ein Zertifikat beantragen, auch wenn die Module, die für die Ausstellung erforderlich sind, bereits vor dem 01.10.2022 absolviert wurden.
Weitere Informationen
Ansprechpersonen
PD Dr. Stefan Helfert (Vetretung Dr. Silke Hartlieb), Dr. Daniela Keller, Iryna Petrenko
Telefon: +49 2331 987-2552
E-Mail: studienberatung.mathinf
Sprechzeiten: Montags und donnerstags von 13-16 Uhr
Kurzfristige Änderungen der Sprechzeiten kündigen wir unter Aktuelles für Studierende an.
Ansprechpersonen für die Studiengänge der Wirtschaftsinformatik finden Sie auf den Internetseiten des Prüfungsamtes der Fakultät für Wirtschaftswissenschaft.
